논문정보
Disentangling Label Distribution for Long-tailed Visual Recognition
논문정리
Abstract
롱데일 이미지 인식에서 많은 연구들이 분류 모델을 훈련할때는 롱테일 분포를 가진 소스 데이터로 하고, 평가는 균일한 분포를 가진 테스트 데이터로 수행한다.
하지만 테스트 분포가 롱테일일 수도 있기 때문에 이런 방법은 실용성이 의심스럽다.
따라서, 본 연구진은 롱테일 이미지 인식을 소스와 타겟 레이블 분포가 다른 label shift problem이라 정함
label shift 문제에서 많은 장애물 중 하나는 소스 라벨 분포와 모델 예측간의 entanglement 이기 때문에 이 둘 간의 관계를 disenstangling 하는 것에 초점을 두었다.
먼저 베이스라인으로 cross entropy loss와 softmax로 훈련된 모델의 예측값을 후처리하여 타겟 레이블 분포와 일치시키는 방법을 소개한다.
이 방법조차도 기존의 SOTA보다 낫지만 훈련 중에 모델 예측에서 소스 라벨 분포를 disentangle하면 좀 더 개선될 수 있다.
Donsker-Varadhan representation의 optimal bound에 기반한 새로운 혁신적인 방법 LAbel distribution DisEntangling loss를 제안한다.
LADE는 CIFAR-100-LT, Places-LT, ImageNet-LT, iNaturalist 2018 등 벤치마크 데이터셋에 대해 SOTA성능을 달성하였으며 various shifted target label distribution에 대한 성능은 다른 방법들을 능가한다.
Introduction
Imagenet, COCO, Places 등 대규모 데이터셋에 대해서는 visual recognition 작업에서 상당한 성과를 거두었지만, 이런 균형있는 데이터셋말고 현실 데이터는 long tailed 분포를 갖는다.
head(major) 클래스가 데이터의 대부분을 차지하고 tail(minor) 클래스가 소수의 샘플을 가짐
SOTA를 달성한 모델도 long tailed 분포를 가지는 데이터셋에선 성능이 떨어짐
따라서 이를 위한 많은 연구들이 있었다.
(1) long tailed 소스 데이터 분포 $p_s(y)$에 대해 훈련
(2) 균일한 타겟 데이터 분포 $p_t(y)$에 대해 평가
대부분 이런 방식으로 성능을 보였는데 이런 평가 프로토콜은 비실용적이라고 해당 논문에서 주장
$p_t(y)는 균일 분포나 long tailed 분포 등 임의의 분포라고 가정해야 하기 때문
따라서, 모델을 임의의 $p_t(y)$에 적응하도록 새로운 방법을 찾아냄
라벨 분포 이동 문제의 개념을 long tailed recognition에서 사용하자!
하지만 소스 확률 $p_s(y|x)$에 적합한 모델 예측 $p(y|x;\theta)$를 바로 사용하기에는 문제가 있는데 타겟 확률 $p_t(y|x)$이 $p_s(y)$에서 $p_t(y)$로 이동하기 때문이다. (그림 1.참고)
그림2(a)는 모델예측과 $p_s(y)$간의 entanglement를 보여준다.
모델은 corss entropy(CE) loss와 softmax 함수로 훈련
이 문제를 완화하기 위해서 모델 출력으로부터 $p_s(y)$를 분리시켜 shfit된 타겟 라벨 분포 $p_t(y)$가 주입되도록 하자.
단순하지만 훌륭한 베이스라인 Post-Compensated Softmax (PC Softmax)은 $p(y|x;\theta)$에서 $p_s(y)$을 빼내기 위해 후처리를 거친 후 모델 output 확률과 $p_t(y)$를 통합시킴.
방법은 단순하지만 PC softmax는 long tailed visual recognition에서 SOTA를 달성함
이 방법이 추론 과정에서의 disentanglement 효용성을 입증하였지만 PC Softmax는 더 훈련과정에서 바로 $p_s(y)$를 빼내는 방법으로 더 개선될 수 있다.
이제 novel method를 제안함
LAbel distribution DisEntangling(LADE) loss
LADE는 Donsker-Varadhan (DV) representation을 활용하여 $p(y|x;\theta)$로부터 즉시 $p_s(y)$를 빼낸다.
▶ 그림2(b)에서 확인
훈련 단계에서의 disentanglement가 임의의 타겟 라벨 분포에 적응하는 데 더 좋은 성능을 보여줌
+ LADE가 다양하게 shift된 $p_t(y)$의 데이터셋에서 성능을 평가할 때 임의의 $p_t(y)$에 더 잘 대처함을 보여줌
- 간단하지만 훌륭한 baseline method인 PC Softmax를 소개함. 이는 여러 long-tailed 벤치마크 데이터셋에 대해 SOTA를 달성함
- 훈련 과정에서 소스 라벨 분포를 disentangling 할 수 있는 LADE loss를 제안하여 임의의 타겟 라벨 분포에 적응할 수 있도록 한다.
Method
<Preliminaries>
먼저 CE loss라고 불리는 소프트맥스 회귀 모델을 훈련하기 위한 가장 일반적인 손실을 살펴본다.
$x$ 입력이미지
$y$ 타겟 라벨
$p_s(y)$ 소스(훈련) 데이터 분포
$p_t(y)$ 타겟(테스트) 데이터 분포
$p_\theta(x)[y]$ 모델의 $y$ 클래스에 대한 logit
소프트맥스 회귀 모델은 $p_s(y|x)$를 추정하고 소스와 타겟 라벨 분포가 같을때 잘 작동한다.
즉, $p_s(y)=p_t(y)$
하지만 실제로는 $p_s(y)\neq p_t(y)$
모델이 $p_s(y|x)$를 추정하게 되면, 분포가 바뀌었을 때를 예측할 때는 사용할 수 없음
∵ 베이즈 정리에서 정의된 $p_s(y|x)$와 $p(y)$ 사이의 강한 결합
<PC Softmax : Post-Compensated Softmax>
라벨 분포 이동을 해결하기 위한 가장 직관적인 방법은 $p_s(y)$를 $p_t(y)$로 바꿔버리는 것
본 연구진은 추론 단계에서 logit을 바꿀 수 있는 post-compensation(PC) 전략을 소개한다.
Definition 3.1 (Post-Compensation Strategy)
PC 전략은 아래와 같다.
$p_s(y)$ 모델의 logit과 entangle된 분포
$p_t(y)$ 모델이 통합해야 하는 타겟 분포
이 PC 전략은 새로운 컨셉이 아니다.
다른 논문에서 출력값에 $p_t(y) / p_s(y)$를 곱하는 다른 형태로 다뤄졌음
하지만, 이 PC 전략은 categorical probability assumption을 해치지 않음
$\sum_c p_t(y=c|x) = 1$
PC 전략을 소프트맥스 회귀모델에 적용하여 Post-Compensated Softmax (PC Softmax)라고 명명함
소프트맥스 회귀 모델에서 PC전략은 타겟 데이터 분포에 적응하는데 적합하다.
Theorem 1 (Post-Compensated Softmax)
소프트맥스 회귀 모델이 $p_s(y|x)$를 추정하여 얻은 클래스 y의 logit을 $f_\theta (x)[y]$라 하면, $p_t(y|x)$에 대한 추정은 다음과 같이 공식화할 수 있다.
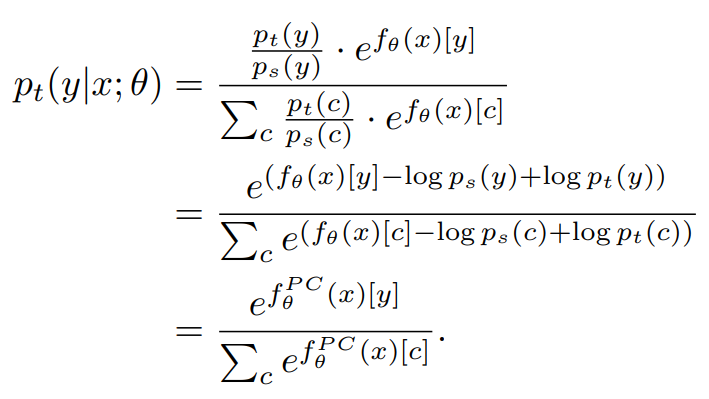
증명은 별첨에 있음
PC softmax는 이전의 SOTA를 능가하는 강력한 베이스라인이지만 최근 연구들에선 이를 베이스라인으로 고려하지 않음
PC Softmax는 Balanced Softmax를 확장한 것으로 볼 수 있다.
Balanced Softmax
훈련 단계에서 균일한 타겟 레이블 분포를 반영하도록 소프트맥스 함수를 변경함
이에 비해 PC Softmax는 추론 단계에서 임의의 타겟 분포 $p_t(y)$와 일치하게 하기 위해서 모델의 logit을 조정함
<LADER : Label distribution DisEntangling Regularizer>
PC 전략의 성능은 소스 라벨 분포를 빼내는 것의 효용성을 보여주었지만 훈련과정에서 이뤄지지는 않는다.
따라서, $p_s(y)$를 대체할 수 있는 새로운 모델링 목표를 설계
두 단계에 걸친다.
- $p_s(y|x)$에서 $p_s(y)$를 분리하여 $p_s(x|y)/p_s(y)$가 될 수 있도록 한다.
- $p_s(x)$의 $p_s(y)$를 균일한 분포를 가진 $p_u(x)$로 대체한다.
$p_u(y=c)= 1/C$ 이때, C는 전체 클래스 개수
최종적으로, 모델의 logit에 대한 모델링 목표는!!!!
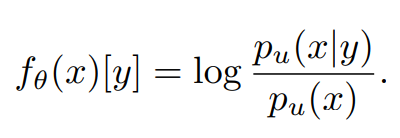
즉, model의 logit이 위 식이 되도록 유도해야함!
위의 로그우도 비율을 명시적으로 모델링하기 위해 정규화된 DV representation의 optimal form을 활용함
DV (Donsker-Varadhan)
Theorem 2 (Optimal form of the regularized DV representation)
$\mathbb{P,Q}$를 임의의 분포라 하자. 이때, $supp(\mathbb{P}) \subseteq supp(\mathbb{Q})$
어떤 도메인 $\Omega$에 대해 모든 함수 $ T : \Omega \rightarrow \mathbb{R}$를 가정
이때 정규화된 DV reprensenation을 최소화하는 함수 $T$는 $\mathbb{P,Q}$의 로그우도 비율이다.
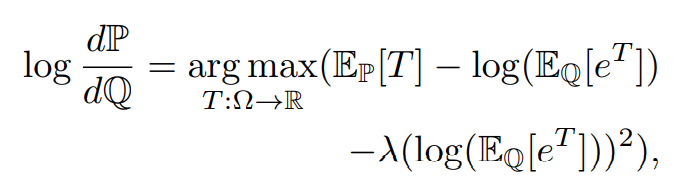
exprectation이 유한하다면 어떤 $\lambda \in \mathbb{R}^+$에 대해 만족
증명은 별첨에 있음
후엥 너무 어려워서 이부분은 스킵할렝,,, 모야이게,,,,,
아무튼 목표는 logit을 정규화하는 새로운 손실을 유도했다는건데 너무어려우엉
Definition 3.2 (LADER)
단일 배치의 샘플 라벨 쌍 $(x_i, y_i)$에 대해 $(i=1,\cdots,N)$ LADER은 아래와 같이 정의
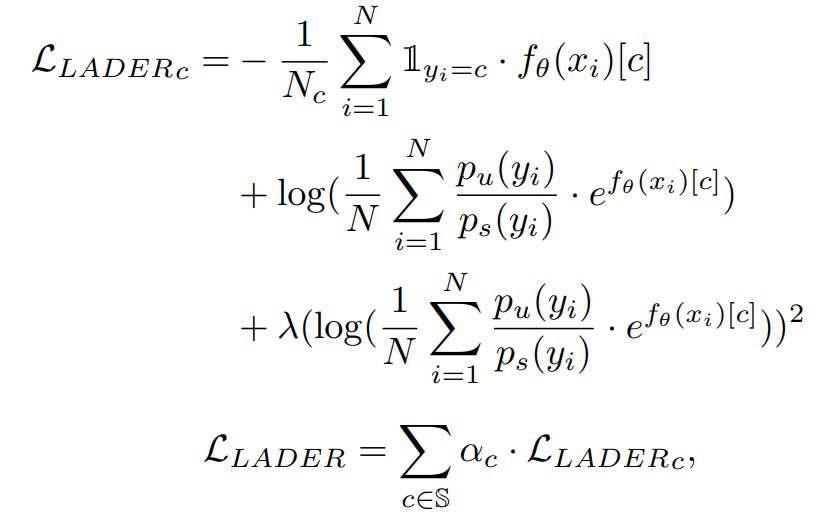
$\lambda, \alpha_1, \cdots, \alpha_C$ ($C$는 총 클래스 개수) 음수가 아닌 하이퍼파라미터이다.
$N_c$ 클래스 $c$의 샘플 수
$\mathbb{C}$ 배치 안에 있는 클래스 집합
<Deriving the conditional probability from disentangled logits>
LADER은 logit이 $log(p_u(x|y)/p_u(x))$가 되도록 규제(regularize)하여 logit이 소스 라벨 분포 $p_s(y)$와 얽히지 않음을 보여준다.
규제된 logit으로 임의의 데이터 분포 $p_t(x,y)$의 조건부확률 $p_t(y|x)$를 평가하기 위해 $p_t(x|y)=p_u(x|y)$라 가정하고 베이즈 법칙으로부터 유도된 수정된 Softmax 를 사용한다.
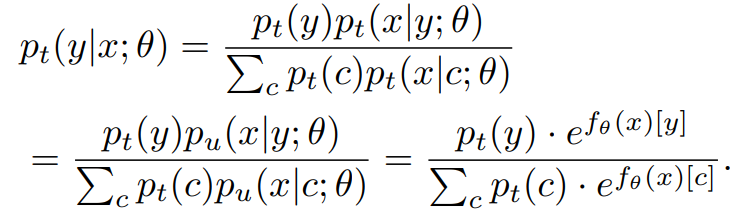
이것과 비슷하게, 식17에서 $p_t(y)$를 $p_s(y)$로 바꿔 $p_s(y|x)$를 평가하면 $p_s(y|x;\theta)$는 CE loss에 의해 최적화된다.
따라서, LADE를 CE loss와 결합하여 훈련을 위한 최종 loss를 결정
Definition 3.3 (LADE)
LAbel distribution DisEntangling (LADE) loss 는 다음과 같이 정의한다.
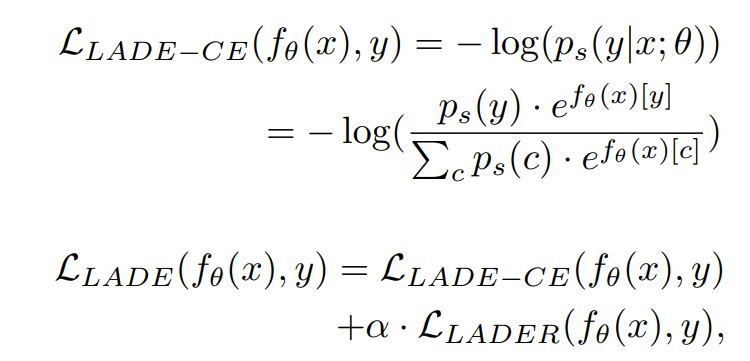
$alpha$ 음수가 아닌 하이퍼파라미터, $\mathcal{L}_{LADER}$의 정규화정도를 결정
Balanced Softmax는 $\alpha=0$일때 LADE와 동일하다.
하지만, LADE는 logit을 직접적으로 규제하여 전체적으로 다른 관점으로부터 나온 개념임
게다가, Balanced Softmax는 오로지 타겟 라벨 분포가 균일할때만을 다루지만 본 논문에서 제안된 방법은 재훈련 없이도 임의의 타겟 라벨 분포를 다룰 수 있다.
추론 과정에서, 타겟 라벨 분포는 식 17에서처럼 inject한다.