구름 운형을 분류하는 딥러닝 모델을 만들고 있는데,
수집된 데이터의 샘플 불균형이 너무 심한 탓인지 테스트 셋에 대한 결과가 좋지 않았다.
이에 대해서 업샘플링을 진행할까 해봤는데 해당 논문이 도움이 될 것 같아 읽어보기로 하였다.
정리된 것도 많고 구현된 코드도 있어서 good
논문정보
Class-Balanced Loss Based on Effective Number of Samples
논문정리
Abstract
대용량의 데이터셋이 빠르게 증가하게 되면서, long-tailed 데이터 분포 문제를 해결하는 것이 중요해졌다.
long-tailed 이란?
소수의 클래스가 데이터의 대부분을 차지하고 나머지 클래스는 데이터가 부족한 경우
기존의 해결책은 re-sampling, re-weighting같은 전형적인 re-balancing 방법들이다.
해당 논문에선 샘플의 수가 증가할수록, 추가적으로 얻을 수 있는 정보의 양은 줄어든다는 것에 주의하였다.
각 샘플을 하나의 포인트보다는 인접 영역과 연관시켜서 data overlap을 측정하는 새로운 프레임워크 소개
샘플의 effective number는 샘플의 볼륨으로 정의되며, $(1-\beta^n)/(1-\beta)$의 간단한 식을 통해 계산된다.
$n$은 샘플의 수이며 $\beta$는 [0,1)인 하이퍼 파라미터
연구진은 각 클래스에 대한 샘플의 effective number를 이용해서 손실을 re-balance하여 class-balanced loss를 얻을 수 있는 re-weighting scheme를 소개한다.
실험은 long-tailed CIFAR 데이터셋과 ImageNet, iNaturalist 데이터셋을 이용한다.
long-tailed 데이터셋에 대해 제안된 class-balanced loss를 사용했을 때, 네트워크가 상당한 성능을 달성한 것을 보여준다.
Introduction
이미지 인식 분야에서 심층 CNN의 성공은 대용량 데이터셋을 사용하게 된 덕이 크다.
일반적으로 사용되는 이미지 인식 데이터셋(CIFAR, ImageNet, ILSVRC 2012, CUB-200 Birds)과 달리, 현실 세계의 데이터셋은 long-tail을 갖는 skewed 분포를 가지고 있다.
언급된 데이터셋은 각 클래스에 대해서 균등한 분포를 가짐
이런 데이터로 훈련된 CNN은 샘플 수가 적은 클래스에 대해서는 성능이 떨어진다.
최근의 많은 연구들이 long-tailed 훈련 데이터의 문제점을 완화시키려 노력하였다.
일반적으로 re-sampling과 cost-sensitive re-weighting의 두 가지 전략이 있다.
- re-sampling : 샘플의 수를 맞추는 것인데 데이터수가 적은 클래스(minor class)를 over-sampling하거나, 데이터가 많은 클래스(major class)를 uner-sampling하는 방법이 있다.
- cost-sensitive re-weighting : minor class에게 더 큰 가중치를 부여하여 손실함수를 보정한다.
CNN을 사용한 심층 특징 표현의 경우, re-sampling은 over-sampling 시 중복된 샘플이 많아 훈련 속도를 느리게 하며, 모델이 과적합에 취약하게 된다. 이런 단점때문에 해당 논문에서는 re-weighting 에 집중하였다.
즉, 어떻게 더 나은 class-balanced loss를 설계할 것인가.
일반적으로 class-balanced loss는 클래스 빈도에 반비례하게 샘플 가중치를 할당한다.
이 방법은 많은 곳에서 사용되었다.
하지만, 최근 연구에서는 대규모 long-tailed 데이터셋에 대해 이런 방법을 사용했을 때 성능이 좋지 않은 것을 보여주었다.
따라서 그들은 클래스 빈도의 제곱근에 반비례하게 설정된 "smoothed" 가중치를 사용하였다.
이제 질문을 제시한다.
어떻게 하면 다양한 데이터셋에 적용할 수 있는 더 나은 class-balanced loss를 설계할 수 있을까?
연구진들은 샘플 크기의 관점에서 답한다.
그림 1을 보면, major class와 minor class를 구분하기 위해 모델을 훈련한다.
데이터 불균형이 심하기 때문에 모델을 바로 훈련(회색 실선)하거나, 샘플수의 역으로 손실을 re-weighting 했을 때(빨간 점선)는 만족스러운 성능을 내지 못한다.
직관적으로는 데이터가 많을 수록 좋다.
하지만, 데이터 간 정보가 겹치기 때문에 (data overlap) 샘플 수가 증가하면 모형이 추출할 수 있는 marginal benefit이 줄어들게 된다.
이를 해결하기 위해, 손실 함수에 샘플의 effective number에 반비례하는 class-balanced re-weighting 항이 추가된다.
이 경우, CNN으로 long-tailed 데이터셋을 훈련했을 때 손실함수의 성능을 크게 향상시킨 것을 확인하였다.
Key Contrubition
- 샘플의 effective number을 연구하고 long-tailed 훈련 데이터셋을 다루기 위해 class-balanced 항을 설계하여 이론적 프레임워크 제공
- 현재 주로 사용되는 손실함수(softmax cross-entropy, sigmoid cross-entropy, focal loss)에 제안된 class-balanced 항을 추가하면 성능을 상당히 향상시킨 다는 것을 증명
게다가, class-balanced loss가 이미지 인식 분야에서 generic loss로 사용 될 수 있음
ILSVRC 2012데이터에 대해 softmax-entropy loss의 성능을 넘었음
Related Work
<Re-Sampling>
over-sampling은 minor class에서 샘플을 더하는데 모델이 과적합 도힐 수 있다.
이를 해결하기 위해 인접한 샘플로부터 샘플을 보간하거나 마이너 클래스를 합성할 수 있지만 샘플의 노이즈가 오류를 야기할 수 있다.
따라서, 중요한 샘플이 제거되는 위험이 있더라도 over-sampling보다는 under-sampling이 더 선호된다.
<Cost-Sensitive Learning>
주어진 데이터 분포와 일치시키기 위해 샘플에 가중치 할당
데이터 불균형이 있는 데이터셋의 경우, 클래스 빈도의 역으로 가중치를 부여하는 것이나, 제곱근의 역으로 가중치를 부여하는 smoothed version이 많이 쓰인다.
본 연구진은 (a) 샘플의 effective number를 정량화 하는 방법과 (b) re-weighting loss에 이를 사용하는 방법에 집중한다.
또한, 샘플의 difficulty를 연구해, hard example에 대해 더 높은 가중치를 부여하는 것이 목표
minor class의 샘플은 major class에 비해 더 높은 손실을 갖는다.
하지만, 샘플 난이도와 샘플의 수 사이에는 직접적인 연관은 없다.
hard example에 더 높은 가중치를 부여하는 것의 단점은 잡음이나 라벨링되지 않은 데이터와 같은 harmful data에 집중하게 된다는 것.
해당 연구에서는, 데이터 분포와 난이도에 대한 어떤 가정도 만들지 않는다.
class-balanced 항을 추가해 focal loss를 개선하여 샘플 난이도에 기초해 re-weighting을 보완하는 것을 보여줌
<Covering and Effective Sample Size>
본 연구의 이론적 프레임워크는 random covering problem의 영향을 받았고, 무작위의 작은 집합의 시퀀스로 큰 집ㅎ바을 커버하는 것이 목표.
논문에서 제안된 샘플의 effective number는 통계학에서의 effective sample size와는 다르다.
Effective Number of Samples
데이터 샘플링 과정을 random covering의 간소화된 버전으로 수식화한다.
주요 아이디어는 각 샘플을 하나의 포인트보다는 작은 이웃 영역과 연관시킨다는 것
<Data Sampling as Random Covering>
클래스가 주어지면, 해당 클래스에서 특징 공간에 있는 모든 가능한 데이터 집합을 $\mathcal{S}$로 표기
$\mathcal{S}$의 볼륨을 $N$이라고 하자 $N \geq 1$
즉, $N$은 모든 데이터 수
각 데이터를 단위 부피가 1이고 다른 데이터와 겹칠 수 있는 $\mathcal{S}$의 하위 집합으로 표시
영역이기 때문에 overlap 될 수 있음
데이터 샘플링은 각 데이터(subset)가 $\mathcal{S}$로부터 랜덤하게 샘플링 되는 random covering 문제로 간주
데이터가 샘플링 될 수록 $\mathcal{S}$를 채우게 된다.
샘플 데이터의 예상 총 볼륨은 데이터 수가 증가할수록 커지며 $N$으로 제한된다.
Definition 1 : Effective Number
샘플의 effective number는 샘플의 예상 볼륨!
샘플의 예상 볼륨(expected volume)을 계산하는 것은 샘플의 shape와 특징공간의 차원에 따라 달라지는 어려운 문제임
문제를 다루기 쉽게 만들기 위해서는, 부분적으로 겹쳐지는 상황을 고려하지 않는 문제로 단순화시킴
즉, 새롭게 샘플링된 데이터는 이전에 샘플링된 데이터와만 다음의 두 가지 방식으로 교류한다고 가정
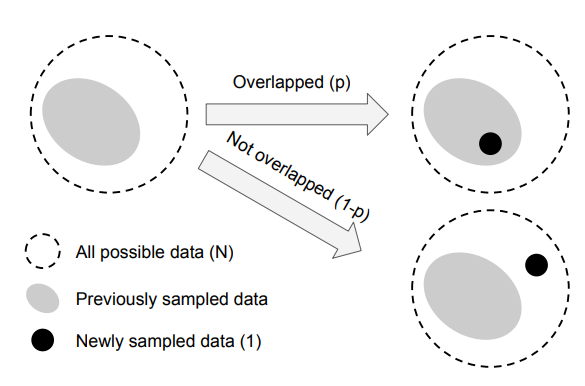
- 이전에 샘플링된 데이터셋 전체 내부에 속할 확률 $p$
- 외부일 확률 $1-p$
샘플된 데이터 포인트 수가 증가할수록 확률 $p$는 증가한다.
수학적 공식을 이해하기 전에, effective number와 현실 세계의 이미지 데이터간의 연관성을 알아보자.
아이디어는 더 많은 데이터 포인트를 이용하여 margfinal benefits이 감소하는 것을 포착하는 것!
데이터가 적은 class에 해당하는 데이터가 추가되면 새롭게 추가되는 정보는 많을 것입니다.
각 데이터가 영역을 갖고 있다고 가정할 시에 다른 데이터와 overlab 될 확률이 적기 때문입니다.
반대로 데이터가 많은 class에 해당하는 데이터가 추가되면 해당 데이터는 다른 데이터와 overlab 될 확률이 많습니다.
이는 새로운 데이터가 새로운 정보를 거의 포함하고 있지 않다는 것을 의미합니다.
출처 : https://deep-learning-study.tistory.com/671?category=1003905
현실세계의 데이터는 본질적인 유사성으로 인해서 (비슷비슷) 샘플 수가 많으면 새로운 샘플이 기존 샘플과 겹칠 가능성이 커짐
CNN은 random crop, 크기 조정, 수평 뒤집기와 같은 간단한 변환으로 입력 데이터를 증강하여 훈련함
이 경우는, 증강된 데이터도 기존의 데이터와 동일한 것으로 간주됨
데이트 증대를 많이 할 수록 $N$은 더 작아질 것 (왜징..)
샘플의 작은 인접 영역은 근처의 유사하거나, 데이터증강으로 얻은 인스턴스를 포착하는 방법임.
클래스의 경우, $N$을 고유한 프로토타입의 수로 볼 수 있다.
<Mathematical Formulation>
샘플의 effective number (expected volume)을 $E_n$으로 표기 (이때, $n \in \mathbb{Z}_{>0}$ 은 샘플 수)
Proposition 1 : Effective Number
$E_n = (1-\beta^n)/(1-\beta)$, where $\beta = (N-1)/N $.
증명
귀납법으로 명제 증명.
$E_1 = 1$ 인 것은 분명하다
전혀 겹치는 부분이 없기 때문
따라서, $E_1 = (1-\beta^1)/(1-\beta)=1$
다음으로, $n-1$개의 예제를 샘플링하였고 $n$번째 예제를 샘플링하려는 일반적인 상황에 대해 살펴보자
이전에 샘플링된 데이터의 예상 볼륨은 $E_{n-1}$이며, 새롭게 샘플링 될 데이터 포인트는 $p=E_{n-1}/N$의 확률로 이전의 샘플과 겹쳐질 것이다.
따라서, $n$번째 샘플링 한 후의 예상 볼륨은
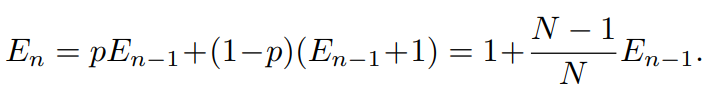
p확률로 겹치게되면 effective number은 그대로 $E_{n-1}$일테고,
1-p확률로 겹치지 않으면 effective number은 $E_{n-1}$에서 1개 증가하게 될 것
$E_{n-1} = (1-\beta^{n-1})/(-\beta)$이므로
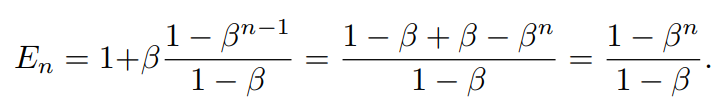
위 명제는 effective number가 $n$에 대한 지수함수임을 보여준다.
이때 하이퍼파라미터 $\beta\in[0,1)$는 $n$이 증가할수록 $E_n$이 얼마나 빨리 커지는지를 결정한다.
effective number에 대한 다른 표현방법도 있다.
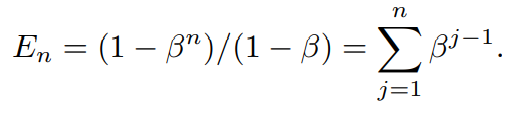
$j^{tj}$샘플이 effective number에 $\beta^{j-1}$만큼 기여함을 의미
N에 대한 총 볼륨은 다음과 같이 계산된다.
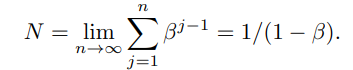
$\beta$에 대한 명제와 일치하다.
Implication 1 : Asymptotic Properties
$E_n = 1$ if $\beta=0 (N=1).$
$E_n\rightarrow n$ as $ \beta \rightarrow 1(n\rightarrow \infty).$
증명
$\beta=0$ 이라면 $E_n=(1-0^n)/(1-0)=1$
$\beta\rightarrow 1$인 경우를 $f(\beta)=1-\beta^n$ and $g(\beta)=1-\beta$라 표기함
$\lim_{\beta\rightarrow 1}f(\beta)=\lim_{\beta\rightarrow 1}g(\beta)=0$이므로 $g'(\beta)=-1\neq 0$이고 $\lim_{\beta\rightarrow 1}f'(\beta)/g'(\beta)=\lim_{\beta \rightarrow 1}(-n\beta^{n-1})/(-1) = n$
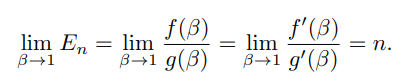
즉, $E_n$은 $N$이 커질수록 샘플의 개수인 $n$에 가까워짐을 의미한다.
고유한 프로포타입 $N$이 크다면, 겹치는 데이터가 없고 모든 샘플이 고유하다고 간주할 수 있다.
다른 극단적인 예인 $N=1$인 경우는, 하나의 프로포타입만 존재하고 따라서 해당 클래스의 모든 데이터는 데이터 증강이나 변환을 하면 해당 프로포타입으로 표현됨을 뜻한다.
Class-Balanced Loss
Class-Balanced Loss는 effective number에 반비례한 가중치요소를 소개하여 불균형한 데이터로 훈련하는 문제를 해결하기 위해 고안되었다.
클래스 균형 손실항은 광범위한 심층네트워크나 손실함수에 적용할 수 있다.
입력샘플 $\mathbf{x}$에 라벨 $y\in \{1,2,\cdots,C\}$이 있을 때 (이때 $C$는 총 클래스 개수), 모델이 예측한 클래스 확률이 $\mathbf{p}=[p_1, p_2, \cdots,p_C]^T$라고 하자
$C$는 총 클래스 개수
$p_i \in [0.1] \,\forall i$
손실은 $\mathcal{L}(\mathbf{p},y)$로 표기한다
클래스 $i$에 대한 샘플 개수를 $n_i$라 하면, 식2에 의해 해당 클래스 $i$에 대한 effective number는 $E_{n_i}=(1-\beta^{n_i}_i)/(1-\beta_i)$
이때 $\beta_i = (N_i-1)/N_i$
해당 클래스에 대한 추가 정보가 없으면 하이퍼 파라미터 $N_i$에 대해 경험적으로 좋은 값을 찾기 어렵다.
그러므로 사전에 $N_i$을 데이터셋에 관련된 값으로 설정한다.
$N_i = N, \beta_i=\beta=(N-1)/N$
손실에 균형을 맞추기 위해서 클래스 $i$의 effective number에 역비례하는 가중치 인자 $\alpha_i$를 소개한다.
$\alpha_i \propto 1/E_{n_i}$
$\alpha_i$를 적용할 때, total loss를 같은 규모로 만들기 위해 $\alpha_i$를 정규화한다
$\sum^C_{i=1} \alpha_i=C$가 되도록
간결성을 위해, 논문의 나머지 부분에선 정규화된 가중치 인자를 $1\E_{n_i}$로 표기한다.
클래스 $i$에 대한 샘플이 주어지면 손실함수에 가중치 인자 $(1-\beta)/(1-\beta^{n_i}$를 더한다
하이퍼파라미터 $\beta \in[0,1)
class-balanced(CB) loss는 다음과 같이 쓰인다
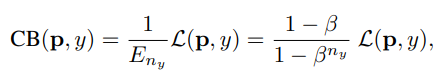
$n_y$는 ground-truth 클래스 $y$의 샘플 수
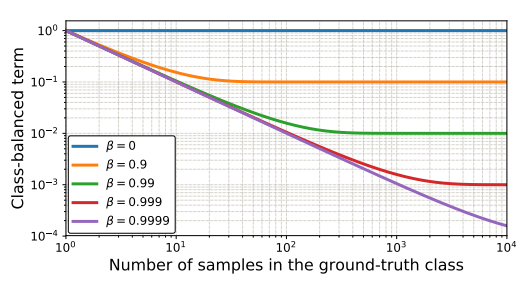
그림 3은 CB손실을 시각화 한 것이다.
$\beta=0$은 re-weighting을 하지 않은 것을 의미하며 $\beta\rightarrow 1$은 class frequency의 역으로 re-weighting한 것
effective number의 개념은 하이퍼 파라미터 $\beta$를 사용하여 CB loss 항을 re-weighting을 하지 않은 것과 한 것 중에 조정하도록 한다.
제안된 CB항은 손실함수 $\mathcal{L}$과 예측된 클래스 확률 $\mathbf{p}$에 독립적이기 때문에 모델에 구애받지 않고, 손실함수에도 구애받지 않는다.
제안된 CB loss를 좀 더 일반적으로 만들기 위해서 3가지 손실함수에 대해 어떻게 적용하는지 보여주겠다.
softmax cross-entropy loss, sigmoid cross-entropy loss, focal loss
<Class-Balanced Softmax Cross-Entropy Loss>
모델의 예측값은 $\mathbf{z}=[z_1, z_2, \cdots,z_C]$ ($C$는 클래스 총 개수)
소프트맥스 함수는 각 클래스를 상호배타적으로 간주하고, 각 클래스에 대한 확률분포를 구한다
$p_i = exp(z_i)/\sum^C_{j=1}exp{z_j},\forall i \in {1,2,\cdots,C}$
레이블 $y$인 샘플이 주어지면, softmax cross-entropy(CE) loss는 다음과 같다
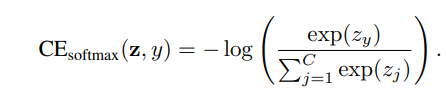
$y$에 $n_y$개 만큼 훈련샘플이 있다면, CB softmax cross-entropy loss는 다음과 같다
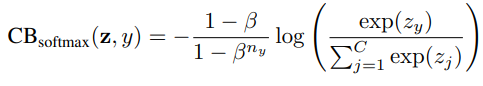
<Class-Balanced Sigmoid Cross-Entropy Loss>
소프트맥스와 달리, 시그모이드 함수에 의한 클래스 확률은 각 클래스가 독립적이고 상호배타적이지 않다고 가정하고 계산된다.
시그모이드 함수를 사용하면, 다중클래스에 대한 이미지 인식문제를 multible binary 분류 문제로 간주한다
이때 각 출력노드는 나머지 클래스에 대한 해당클래스의 확률을 예측하기 위해 one-vs-all 분류를 수행함
소프트맥스와 다르게, 시그모이드를 쓰면 real-world 데이터셋에 대해 두가지 장점이 있다.
- 시그모이드는 상호배타성을 가정하지 않으므로 실제 데이터와 잘 어울린다. 즉, 소수의 클래스가 다른 클래스와 매우 유사할 수 있다.
- 각 클래스가 독립적이라 간주되고 own predictor를 가지므로, 시그모이드는 single-label 분류와 multi-label 예측을 합친다. 실제 데이터에는 하나 이상의 라벨을 가지는 경우가 있으므로 좋은 특성이다.
소포트맥스 크로스엔트로피에서 쓰인 표기법을 이용하여 $z^t_i$를 다음과 같이 정의한다
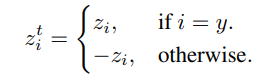
sigmoid cross-entropy(CE) loss는 다음과 같이 쓰인다.
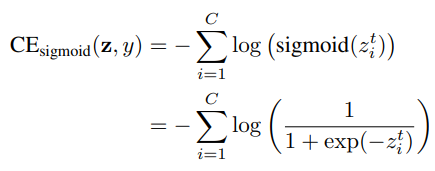
class-balanced(CB) sigmoid cross-entropy loss는 다음과 같다
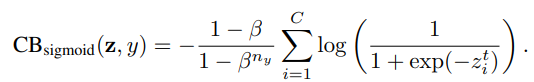
<Class-Balanced Focal Loss>
최근에 제안된 focal loss(FL)는 시그모이드 크로스엔트로피 손실에 조절인자를 추가하여 잘 분류된 샘플에 대해 relative loss를 줄이고 다른 샘플에 주의한다.
$p^t_i=sigmoid(z^t_i)=1/(1+exp(-z^t_i))$로 표기하고 focal loss는 다음과 같이 쓰인다
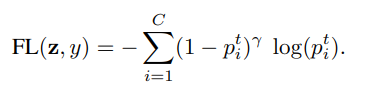
class-baanced(CB) focal loss는 다음과 같다
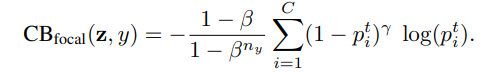
기존의 focal loss에는 $\alpha$-balanced 변종이 있다.
class-balanced focal loss는 $\alpha$-balanced focal loss라 볼 수 있다.
다만, 이때 $\alpha_t=(1-\beta)/(1-\beta^{n_y})$
그러므로, class-balanced항은 effective number을 기반으로 $\alpha_t$를 조절하는 방법이라고 볼 수 있다.
실험부분은 생략하였다.
코드는 GitHub - richardaecn/class-balanced-loss: Class-Balanced Loss Based on Effective Number of Samples. CVPR 2019 에서 확인할 수 있다.
GitHub - richardaecn/class-balanced-loss: Class-Balanced Loss Based on Effective Number of Samples. CVPR 2019
Class-Balanced Loss Based on Effective Number of Samples. CVPR 2019 - GitHub - richardaecn/class-balanced-loss: Class-Balanced Loss Based on Effective Number of Samples. CVPR 2019
github.com
단, 텐서플로우임
데이터는 Long-tailed CIFAR을 사용하였다.