이번 논문은 영어 논문이라 빠르게 읽고 요약하는 것이 힘들 것 같아 천천히 해석하면서 공부해보려고 한다.
Glove 라는 모델의 설명인 것 같다. 12페이지 분량의 논문이다. ㅠㅠ 시작해보자 화이팅.
<ppt 정리한 게시물>
GloVe 논문 ppt 정리
논문 발표를 위해 ppt로 정리한 부분이 나중에 볼때 도움 될 것 같아 업로드한다. 나는 , 을 맡았고 그 외 part는 다른 팀원분들이 제작하였기 때문에 내가 만든 부분만 올리겠다.
haystar.tistory.com
논문정보
Glove : Global Vectors for Word Representation
논문정리
Abstract
이때까지, 최신 연구들에서 의미와 구문 규칙을 파악하는 것은 성공했지만, 그 규칙에 대한 origin은 불분명하다.
이 논문은 이런 규칙이 단어 벡터에 표현되는데 필요한 모델의 특성들을 분석하고 명시한다.
결과 모델은 새로운 global log bilinear 회귀모델 (두 가지 모델의 장점을 결합함)
word-word 동시발생 매트릭스의 0이 아닌 원소들만을 훈련하여 통계적 자료를 효과적으로 활용한다.
모델은 의미 있는 하위 구조를 가진 벡터 공간을 생성하고, 단어 유추 작업에서 그 성능은 75% 정도이다.
Introduction
언어의 의미 벡터 공간 모델에서 각 단어는 실수 벡터로 표현된다.
대부분은 벡터의 성능을 평가하기 위해 단어 벡터 쌍 사이의 거리나 각도를 이용하였다. 최근에, mIkolov가 단어 유추에 기반한 새로운 평가 쳬계를 도입하였는데, 단어벡터 간 스칼라 거리가 아닌, 각 차원의 차이를 조사하여 단어 벡터 공간의 미세구조를 확인한다.
"King is to queen as man is to man"라는 비유는 벡터 공간에서 벡터 방정식 "king - queen = man - woman"으로 암호화된다.
단어 벡터를 학습하는 주 모델은 다음과 같다.
1) global matrix factorization methods, such as LSA(latent semantic analysis)
2) local context window methods, such as the skip-gram model
위 모두 심각한 단점을 겪는다.
LSA 같은 경우는, 통계자료를 효과적으로 사용하지만, 단어 유추 작업을 제대로 수행하지 못한다.
Skip-gram의 경우는, 유추 작업에서는 더 낫지만, 말뭉치의 통계자료를 제대로 활용하지 못한다.
(global 동시발생 횟수 대신에 지역적인 context window에 대해서 훈련하기 때문)
본 연구에서는, global log bilinear 회귀모델이 적합하다고 보며 global word-word co-occurrence count를 훈련한 specific weighted least squares 모델을 제안한다.
소스코드는 http://nlp.stanford.edu/projects/glove/. 에서 확인할 수 있다.
Related Work
<Matrix Factorization Method> - 행렬 분해
저차원 단어 표현을 생성하는 행렬분해법은 LSA처럼 뒤로 뻗은 root를 가진다.
이 방법은 낮은 등급의 근사치를 이용하여 말뭉치의 통계적 정보를 가지는 큰 행렬을 분해한다.
매트릭스에 담긴 정보의 유형은 응용에 따라 다르다.
LSA의 경우 행렬 유형은 "term - document"이다. 하나의 행은 단어나 용어를 가리키고 열은 말뭉치의 다른 문서에 해당한다.
HAL의 경우, 행렬 유형은 "term - term"이며 행과 열 모두 용어를 가리킨다. 개체는 context내에서 다른 단어가 주어졌을 때 한 단어가 나타나는 횟수에 해당한다. (HAL : Hyperspace Analoogue to Language)
HAL과, 이와 연관된 방법의 주요 문제는 가장 빈번하게 나타나는 단어들이 유사도 측정값을 크게 좌우한다는 것이다.
ex) and와 the가 동시에 발생하는 횟수는 의미론적인 관련성을 보여주진 않지만 유사도에 큰 영향을 준다.
이런 단점을 극복하기 위한 기술들이 많이 존재하는데, 동시발생 행렬이 엔트로피나 상관관계에 기반하여 변환된다.
이렇게 변환하면 동시발생 횟수가 더 작은 간격에서 고르게 분포되도록 압축된다.
최근에는 HPCA 형태의 제곱근 변환이 효과적인 단어 표현 학습 방법으로 제안되었다. (HPCA: Hellinger PCA)
<Shallow Window-Based Method>
다른 접근법은 지역적인 문맥 창(context window) 내에서 예측에 도움이 되는 단어들을 학습하는 것이다.
최근 들어, 유용한 단어 표현을 학습하기 위한 전체 신경망 구조의 중요성에 의문이 제기되고 있다.
Skip-gram과 CBOW모델은 두 단어 벡터 사이의 내적에 의한 단일 레이어 구조를 제안한다.
(CBOW : Continuous Bag-of-Words)
vLBL, ivLVL은 또한 밀접하게 관련된 vector log bilinear 모델이다.
Skip-gram과 ivLBL 모델의 목적은 단어 그 자체를 통해 단어의 문맥을 예측하는 것에 있으며,
CBOW와 vLBL모델은 문맥을 통해 주어진 단어를 예측하는 데 있다.
단어 유추 작업에 대한 평가를 통해, 단어 벡터사이의 선형 관계로 언어 패턴을 학습할 수 있는 능력이 입증됨.
https://haystar.tistory.com/19 여기서 다룬 적 있음.
주변 단어가 주어졌을 때 목표 단어를 학습하는 방식 (CBOW)
목표 단어가 주어졌을 때 주변 단어를 학습하는 방식 (Skip-gram)
행렬 분해 방법과 달리, shallow window-based 방법은 말뭉치의 동시발생 통계에 직접 작용하지 않는다는 단점이 있다. 이런 모델은 전체 말뭉치의 문맥 창을 스캔하여, 방대한 데이터의 반복을 활용하지 못한다.
한마디로, 문맥은 잘 파악하지만 통계자료를 활용하지 못한다.
The Glove Model
말뭉치 내의 단어 발생 통계는 비지도방법으로 단어 표현을 학습하는 데에 있어 정보의 주원천이다.
but 다음과 같은 의문은 여전히 존재한다.
1. 통계로부터 의미가 어떻게 생성되는가?
2. 결과 단어 벡터가 어떻게 그 의미를 표현하는가?
우리는 단어 표현을 위한 새로운 모델을 구성하고 Glovbal Vectors를 GloVe라고 부르기로 한다.
(global 말뭉치 통계가 이 모델에 의해서 직접적으로 파악됨)
먼저, 표기법을 정한다.
X : word- word 동시발생 횟수의 행렬
$X_{ij}$ : X의 항목, 단어 i의 context에서 단어 j가 나타나는 횟수
따라서 $X_i = \sum\limits_{k} X_{ik}$이며, 이는 단어 i의 context내에서 어떠한 단어라도 나타나는 횟수를 의미한다.
마지막으로 $P_{ij} = P(j|i) = X_{ij}/X_i$이며, 이는 단어 i의 context내에서 단어 j가 나타나는 확률을 의미한다.
다음 표는, 60억 단어의 말뭉치에서 선택한 몇 단어들과 타겟 단어 ice와 steam의 동시발생 확률을 보여준다.
이 비율에서 큰 차별점이 없는 water과 fashion은 지우고, 1을 기준으로 큰 값은 ice의 특성과 연관되고 작은 값은 steam의 특성과 연관됨을 확인할 수 있다.

동시발생 확률에서 의미가 추출되는 것을 보여주는 예시로 시작해보자.
관심 있는 두 단어 i와 j를 각각 ice (i)와 steam (j)이라고 해보자. 이 단어들의 관계를 기준 단어 k와의 동시발생 확률을 통해 얻을 수 있다.
ice와는 관련 있고 steam과는 없는 단어 k를 solid라고 하면, $P_{ik}/P_{jk}$ 값은 클 것이다.
같은 방법으로, 반대의 경우 k를 gas라고 하면, 비율의 값은 작을 것이다.
water은 두 타겟단어와 모두 관련이 있고, fashion은 모두 관련이 없기 때문에 비율의 값은 1에 가까울 것이다.
이런 비율을 통해, 관련 있는 단어(solid와 gas)와 관련 없는 단어(water와 fashion)를 구분할 수 있다.
따라서 우리는 확률 그 자체보다는 확률의 비율로부터 단어 벡터 학습을 시작해야 한다.
$P_{ik}/P_{jk}$값이 단어 i, j, k에 따라 달라지므로 다음과 같이 표현할 수 있다.
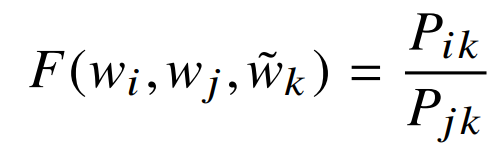
$w$는 단어 벡터이고, $\tilde {w}$는 문맥과 관계없는 단어 벡터이다.
위 등식에서 우변은 말뭉치로부터 구할 수 있고, F는 아직 지정되지 않은 파라미터에 의해 결정된다.
F의 가능성은 매우 크지만, 다음의 방법으로 인해 고유하게 만들 수 있다.
1) F를 단어 벡터 공간에 투영시킴 ($P_{ik}/P_{jk}$를 인코딩)
벡터 공간은 선형구조를 가지므로, 벡터의 차이를 이용한다. (F는 두 대상 단어의 차이에 의존한다)
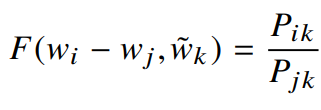
2) F의 인자는 벡터이고, 우변은 스칼라이다. 인자들을 내적 한다.
이렇게 하면 F가 성가시게 벡터의 차원을 혼합하는 일을 방지한다.

3) $w↔\tilde {w}, X↔X^T$
word-word 동시발생 행렬에서 단어와 문맥 단어는 임의로 선택된 것이기 때문에 두 역할을 바꿔줘도 된다.
(바꿔도 결과가 같아야 함 ex) ice와 steam, steam과 ice는 같다)
그러기 위해선 $w$와 $\tilde {w}$뿐만 아니라 $X$와 $X^T$도 교환되어야 한다.
4) 최종 모델은 각 단어를 라벨링 하는 것에 따라 변하지 않아야 한다.
다음과 같은 과정을 거친다.
첫 째로는 F가 Homomorphism하게 한다.
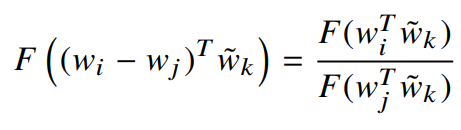
Homomorphism
두 개의 Group 사이의 모든 연산과 관계를 보존하는 사상
아래 링크에 자세하게 나와있다.
늦깎이 공대생의 좌충우돌 이야기 :: Homomorphism(준동형 사상) (tistory.com
여기서식3 을 이용해 풀면 다음과 같이 정리할 수 있다.
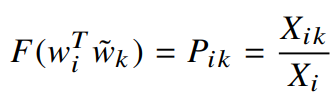
F를 지수함수(homomorphism을 만족하는 함수 중 하나)로 지정한다면 다음과 같이 풀 수 있다.
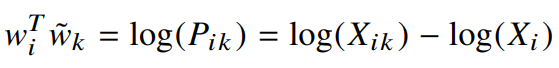
우측의 $log(X_i)$부분을 처리하여 위 수식을 symmetric하게 만들자.
이 항($log(X_i)$)은 k에 대해 독립적이므로 (상수) $w_i$에 대한 bias $b_i$를 더하여 처리할 수 있다.
마지막으로 $\tilde{w_k}$에 대한 bias $\tilde{b_k}$를 더하자.
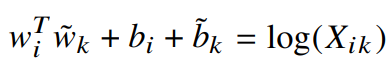
식 1과 비교하면 굉장히 단순해졌지만, 로그함수 특성상 인자가 0이면 발산하기 때문에 정의되지 않는다.
따라서 X의 모든 원소에 1을 더해주면 함수가 발산하는 것을 방지하고 X의 희소성을 유지할 수 있다.
이 결과모델을 실험에서 baseline으로 사용할 것임.
근데, 이 모델에도 단점이 있다.
원래 동시발생행렬에서 0은 75-95%를 차지하게 되는데 이렇게 되면 거의 등장하지 않거나 전혀 나타나지 않는 것들도 똑같은 동시발생 가중치를 갖게 된다. 원래 이런것들은 자주 발생하는 것에 비해 noisy하고 담고 있는 정보량도 적다.
이런 문제를 해결하기 위해 새로운 가중최소제곱 회귀 모델을 제안한다. (V : vocabulary 크기)
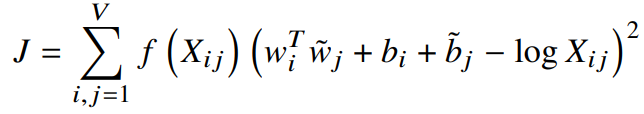
이때, weighting 함수 $f(X_{iu})$는 비용함수이며, 다음의 특성을 만족한다.
1. $f(0) = 0.$
2. $f(x)$는 감소하지 않는다(non-decreasing). 덜 발생하는 단어의 가중치가 더 커서는 안되기 때문.
3. $f(x)$는 매우 큰 값 $x$에 대해 (너무 자주 발생하면) 매우 큰 가중치를 부여하지 않는다.
이러한 특성을 만족하는 함수들은 많지만, 우리는 아래의 f(x)를 사용한다.
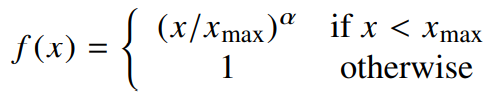
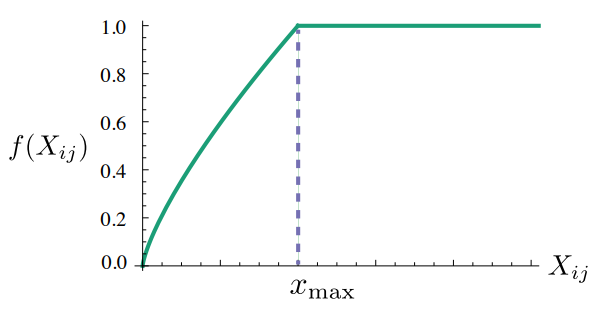
어디서 끊느냐에 따라 성능은 좌우된다. 위에선 $x_{max} = 100$이다.
이때 $\alpha = 3/4$일때가 $\alpha = 1$일 때보다 조금 더 개선된 결과를 보여준다.
<Relationship to Other Models>
단어벡터를 학습하기 위한 비지도방법은 궁극적으로 말뭉치의 출현통계에 기반하기 때문에, 모델들간 공통점이 있다.
이번 절에서는 ivLBL과 skip-gram같은 window-based 방법의 모델이 위에서 제안된 모델과 어떻게 연관되어 있는지 살펴본다.
skip-gram과 ivLBL의 시작점은 단어 i의 context에서 단어 j가 나타날 확률에 대한 모델 $Q_{ij}$이다.
$Q_{ij}$를 softmax함수라고 하자.
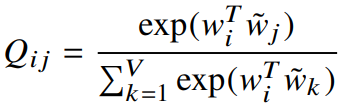
이러한 모델에서, context window에 대한 로그 확률을 최대화하려는 의도는 우리의 목적과 같다.따라서, global 목점함수는 다음과 같이 정의할 수 있다.
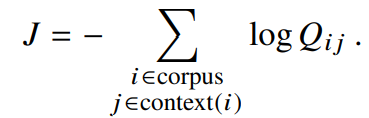
이 합산연산에서 각 항에 대해 소프트맥스 정규화 계수를 얻는 것은 비용이 많이 든다.
효율적으로 훈련하기 위해 skip-gram과 ivLBL 모델은 $Q_{ij}$를 근사한다.
but, 식11의 sum연산은 다음식으로 변환하면 더 빨라진다.
term의 수가 동시발생행렬에서 얻어진다는 것을 이용했다.
식 11은 skip-gram, ivLBL에서 쓰인다고 했다. 이 모델들은 주변단어의 확률을 최대화한다.
그런데 우리는 이미 동시발생행렬에서 주변단어가 주어질 확률을 알고 있다.
i와 j가 같은 경우를 보면 된다.
즉, $X_{ij}$가 미리 연산되어 있기 때문에 연산 속도가 빨라짐.
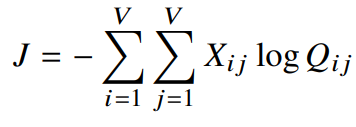
처음에 우리는 $X_i = \sum\limits_{k} X_{ik}$라고 하였다. 그리고 $P_{ij} = X_{ij}/X_i$ 였으니, $J$를 다음과 같이 변형할 수 있다.
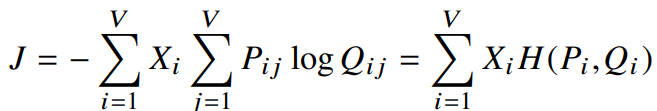
$P_{ij} = X_{ij}/X_i$를 $X_{ij}$에 대한 식으로 변형하면 $X_{ij} = P_{ij}X_i$가 되므로 이를 활용한 것이다.
이때 $H(P_i,Q_i)$는 $P_i, Q_i$분포에 대한 크로스엔트로피다.
but, 아직 단어벡터를 학습하기 위한 모델로 채택되기전에 다뤄야할 부분이 남아있다.
크로스엔트로피의 오차는 확률분포에서 거리를 계산하기 위한 방법 중 하나인데, 꼬리가 긴 확률분포의 경우 잘못 모델링되어서 자주 발생하지 않는 사건에 대해 매우 큰 가중치를 부여하는 경우가 생긴다.
게다가, 측정법에 경계가 있으려면, 모델 분포 Q가 적절하게 정규화되어야 하는데, 그럴 경우 식10의 전체 vocabulary에 대한 sum연산으로 계산병목현상이 나타나기 때문에 다른 거리 측정법을 고려하게 된다.
따라서, 최소제곱법을 선택하게 된다. (P와 Q의 정규화 계수 무시 가능)
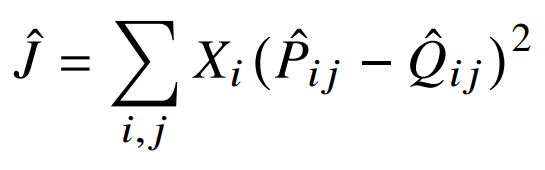
이때, $\hat {P_{ij}} = X_{ij}$, $\hat {Q_{ij}} = exp({w_i}^t\hat {w_j})$은 정규화되지않은 분포이다. 다
그러면 이제는 $X_{ij}$가 가끔씩 매우 큰 값을 가져서 최적화를 방해한다는 문제가 생긴다 (뭐 계속 생기냐..ㅠㅠ)
가장 효과적인 해결책은 로그를 취해 제곱오차의 값을 줄이는 것이다.
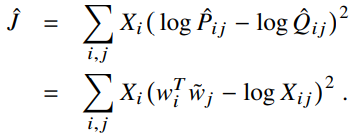
마지막으로, $X_{ij}$는 미리 결정된 가중치 인자인데, 최적화가 보장되지 않는다. Mikolov는 데이터를 필터링하여 성능을 높일 수 있다는 것을 발견했다. 이 점에서, 우리는 문맥단어에 더 의존할 수 있는 보다 더 일반적인 가중치 함수를 제시한다.
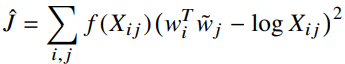
우리가 이전에 유도했던 식8에서의 비용함수와 같다.
<Complexity of the model>
모델의 복잡도는 행렬 X에서 0이 아닌 원소들의 개수에 의해 좌우된다. 그런에 이 수는 행렬의 전체크기보다는 작거나 같을 테니, 모델의 복잡도는 $\mathcal{O}(n^2)$보다 나쁘진 않을 것이다. 처음엔 말뭉치크기 $|C|$의 scale을 갖는 shallow window 기반의 접근법에 비하면 상당히 개선되었다고 생각할 수 있다. 근데 일반적으로 수십만개의 단어들이 있기 때문에 $|V^2|$의 값은 수천억까지 커질 수 있따. 이렇게 되면 말뭉치보다 훨씬 커지게 된다.
X의 0이 아닌 원소 개수를 논하기 위해, 단어 동시발생 분포에 대해 몇가지 가정이 필요하다.
1) 단어 i와 j의 동시발생횟수 $X_{ij}$는 해당 단어쌍의 frequency rank의 멱함수 $r_{ij}$로 나타낼 수 있다.
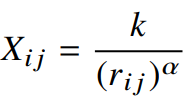
이때, k는 가장 빈도수가 높은 단어의 빈도수이다.
말뭉치 내의 전체 단어 수는 동시발생행렬 X 원소의 총 합에 비례한다.
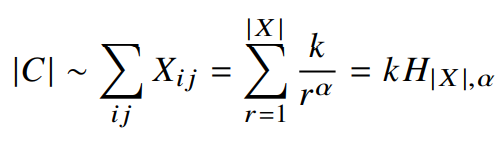
여기서 마지막부분은 일반화된 조화수 $H_{n,m}$로 다시 식을 쓴 것이다. sum연산에서 상한값 $|X|$은 최대 frequency rank이며, 행렬 X의 0이 아닌 원소 개수와 일치한다. 또, 식 17에서 r의 최대값과 같다.
이때, $X_{ij} \geq 1$일때, 단어 rank의 최댓값 $|X|= k^{1/a}$이 된다.
식 17에서 $X_{ij} \geq 1$일때,
$k\geq(r_{ij})^\alpha$
$k^{1/\alpha}\geq r_{ij}$ 인데 $r_{ij}$의 최댓값이 $|X|$이다.
이때, $|X|^\alpha= k$이므로 식 18을 다음과 같이 고칠 수 있다.
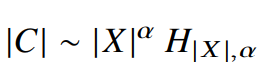
우리는 $|X|, |C|$가 모두 큰 값을 가질 때, 어떤 연관이 있을까 궁금하다. 이 논문은 일반화된 조화수의 확장을 이용하였다.
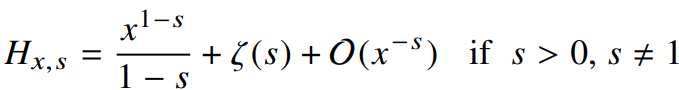
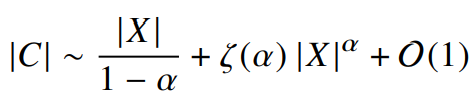
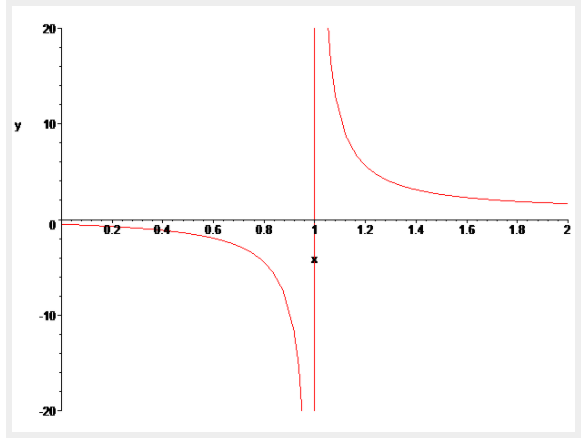
여기서 $\zeta(s)$는 Riemann zeta function이며, X가 매우 큰 값을 가질 때,
식 21 우변의 두 항 중 하나와만 연관을 갖는데 이는 $\alpha>1$을 기준으로 구분된다.
(오른쪽 그래프는 리만제타함수)
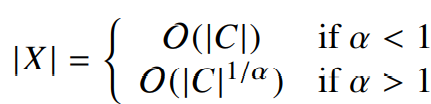
이 실험에서는 $\alpha=1.25$일때, $|X| = \mathcal{O}(|C|^{0.8})$이 되는데 이때 모델의 복잡도가 가장 최악의 경우 였던 $\mathcal{O}(V^2)$보다 훨씬 개선되었다는 것을 관찰했다. 또한, $\mathcal{O}(|C|)$였던 on-line window-based 방법에 비해서도 어느정도 더 나은 결과를 보여주었다.
Expriments
<Evaluation methods>
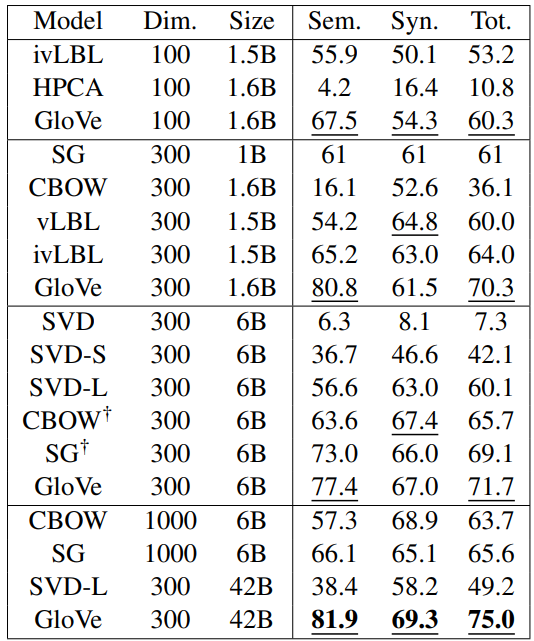
◀ 단어 유추 작업 결과 (표2)
정확도로 주어지고 밑줄친 점수가 비슷한 크기의 그룹 내에서 가장 좋은 점수.
굵은 글자의 점수가 전반적으로 가장 괜찮음.
SG , CBOW는 word2vec을 이용하였음.
단어 유추
단어 유추 작업은 "a와 b의 관계는 c와 ?와의 관계이다."와 같은 질문들로 구성되어 있다.
데이터셋에는 이런 질문들이 19544개 있고, 의미론적인 부분과 구문론적인 부분집합으로 나눠져있다.
의미론적인 질문은 일반적으로 사람과 장소에 대한 유추이다.
ex. "아타네와 그리스의 관계는 베를린과 무엇의 관계일까?"
구문론적인 질문은 동사시제나 형용사 형태의 유사성에 관한다.
ex. "dance가 dancing일때 fly는 무엇이 될까?"
"a와 b의 관계는 c와 ?와의 관계이다."라는 질문에서 코사인유사도를 이용해 $w_b - w_a + w_c$와 가장 가까운 단어 d, $w_d$를 얻는다.
단어 유사도
모델을 아래의 표3에서 단어 유사도 작업의 관점에서도 평가한다. WordSim-353, MC, RG, SCWS, RW등이 포함된다.
개체명 인식
NER용 CoNLL-2003 영문 벤치마크 데이터셋 → 사람, 장소, 조직, 기타 등 4가지 객체 타입에 대해 표기됨.
CoNLL_03 훈련 데이터를 3개의 데이터셋으로 훈련시킨다.
1. CoNLL_03 테스트데이터
2. ACE Phase 2, ACE_2003 데이터
3. MUC7 Formal Run 테스트셋
BIO2 annotaion standard를 따르고, Wang and Manning에 기술된 전처리 과정을 거친다.
437,905개의 별도 특징이 CoNLL-2003 훈련 데이터셋으로부터 생성되었고, 5단어 context 내의 각 단어에 대해 50차원의 벡터가 추가되었고 이는 연속특징으로 사용됨.
이러한 특징들이 입력으로 Wang and Manning의 $CRF_{join}$모델과 동일한 설정으로 CRF를 훈련하였음.
(CRF : Conditional Random field)
<Corpora and training details>
다양한 사이즈의 말뭉치 5개를 모델에 학습하였다. Stanford tokenizer를 이용하여 말뭉치를 토큰화하고 소문자로 바꿔준 뒤 가장 자주 등장한 400,000개에 대한 voabulary를 생성하여 동시발생횟수 행렬 X를 만들었다.
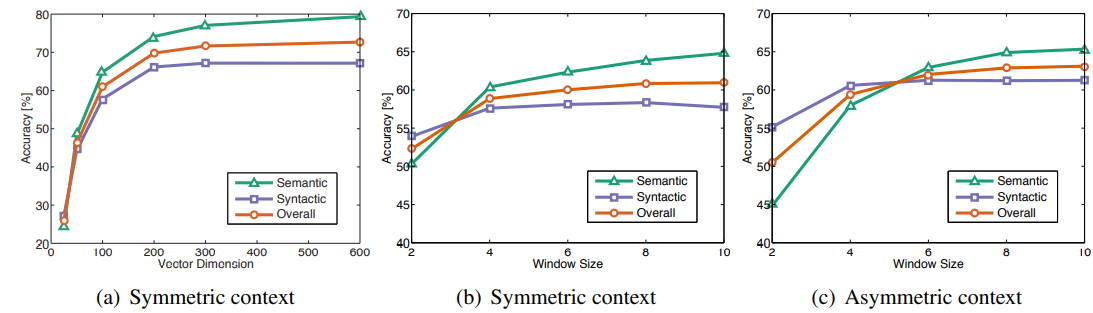
X를 생성할때, context window의 크기와 왼쪽 context와 오른쪽 context를 구분할지에 대한 것을 결정해야 한다.
우리는 감소하는 가중치 함수를 사용하므로 단어 d와 분리된 단어 쌍은 총횟수의 1/d만큼 기여한다. (이게 뭔소리고..)
거리가 먼 단어쌍은 단어 간 관계에 대해 관련성이 낮은 정보를 담고 있을 것으로 예상되는 이유이다.
모든 실험에서 $x_max = 100, \alpha = 3/4$로 정하고 AdaGrad를 이용해 모델을 훈련하였다.
(X의 0이 아닌 원소에 대해 stochastic하게 샘플링하고, 초기 학습률은 0.05로 설정)
300차원보다 작은 벡터에 대해서는 50번반복하고, 반대의 경우는 100번 반복하였다.
별다른 언급이 없을땐, 왼쪽에서 10개의 단어, 오른쪽에서 10개의 단어를 context로 사용하였다.
모델은 두 개의 단어벡터 $W, \tilde{W}$를 생성한다. X가 대칭행렬이면 $W, \tilde{W}$는 랜덤으로 초기화하는 부분만 빼고 동일하다.(두 벡터집합의 성능은 동일함)
특정 신경망의 경우, 네트워크를 여러 인스턴스를 훈련한 뒤 결과를 결합하면 과적합과 잡음을 줄이고 일반적으로는 결과를 개선시킨다고 한다. 그래서 우리는 $W + \tilde{W}$를 단어벡터로 사용하기로 했다. 이렇게하면 성능은 소폭 향상되고 의미적인 유추 작업결과가 가장 크게 개선된다.
다양한 최신 모델의 결과와 Word2Vec를 사용하여 만들어진 결과를 SVD를 이용한 다양한 베이스라인과 비교해본다.
word2vec에선 상위 400,000개의 가장 빈번한 단어들과 context window 크기는 10으로 해서 skip_gram와 CBOW모델로 60억개의 말뭉치를 학습하였다.
SVD 베이스라인에 대해서는, 10000개의 최빈단어를 이용하여 각 단어가 얼마나 자주 발생하는 지에 대한 정보를 유지하는 잘린행렬 $X_{trunc}$을 생성하였다.
이 행렬의 단일 벡터는 SVD를 구성한다. 또한 SVD-S, SVD-L의 두 베이스라인도 평가한다.
(SVD-S는 $\sqrt{X_{trunc}}$의 SVD를, SVD-L은 $log(1+X_{trunc}$의 SVD)
두 방법 모두 X값 범위를 압축시킨다.

