논문정보
Classification of Ground-Based Cloud Images by Improved Combined Convolutional Network
Classification of Ground-Based Cloud Images by Improved Combined Convolutional Network
Changes in clouds can affect the outpower of photovoltaics (PVs). Ground-based cloud images classification is an important prerequisite for PV power prediction. Due to the intra-class difference and inter-class similarity of cloud images, the classical con
www.mdpi.com
운명의 장난인가...☆★
이전에 ECA 모듈 논문을 읽었는데 지금 구름 과제한다고 찾아본 논문이 ECA를 개선했다니 ..!
논문정리
Abstract
구름의 변화는 태양광 출력에 영향을 준다. (그렇겠지,, 구름이 태양을 가려버리면 에너지 흡수가 안되니까,,)
따라서 지상기반 구름이미지 분류가 태양광 출력값을 예측하는 데 중요하다.
구름 이미지는 클래스 내 차이는 적고 클래스 간 유사도가 높기 때문에 이를 구별하기에 기존의 컨볼루션 신경망은 부족하다.
본 논문에선 개선된 결합 컨볼루션 네트워크로 지상 기반 구름 이미지를 분류하는 방법을 제안하였다.
픽셀 정보의 중복으로 인한 하위네트워크 과적합 문제를 막기 위해 overlapping pooling 커널을 사용하여 풀링 레이어에서 중복된 정보를 제거하는 효과를 향상시킨다.
새로운 채널 어텐션 모듈인 ECA-WS (Efficient Channel Attention-Weight Sharing)이 채널 정보를 표현하는 네트워크 능력을 향상시킨다.
결정 융합 알고리즘으로 각기 다른 크기의 하위 네트워크 출력을 융합한다.
각 카테고리 내의 구름 이미지 수를 기반으로 융합 결과에 가중치를 적용하여 네트워크 크기 제한을 해소하고 데이트 불균형을 완화시킨다.
실험은 공개된 MGCD 데이터셋과 자체적으로 구축한 MRELCD 데이터셋을 기반으로 수행
제안된 모델이 기존의 일반적인 네트워크와 최신 알고리즘과 비교했을 때 분류 정확도를 상당히 개선하였다.
Introduction
단기 기상 변화의 영향으로 태양광 발전(PV)의 출력 전력이 쉽게 변한다.
현재는 PV 전력을 예측하여 전력 변동의 영향을 줄이는 방법이 중요하다.
전력 예측을 통해 power sector가 합리적으로 PV 자원을 사용하고, 전력 변동이 그리드에 연결된 PV에 미치는 영향을 감소시킬 수 있다.
구름 덩어리는 단기간에 소실되고 응집되는데 이는 출력 전력의 변동을 주는 주요 요소.
게다가 구름의 종류에 따라 일사량도 바뀐다.
구름종류마다 두께, 고도, 하늘을 덮는 정도 등의 특성이 다 다른데 이로 인해 표면이 받는 태양복사에너지 크기가 달라진다.
따라서 PV 전력 예측을 위해 구름을 제대로 분류하는 것이 중요하다!
같은 카테고리에 속하는 구름들 내에서도 다양한 형태가 존재하고, 서로 다른 카테고리의 구름들 끼리도 유사성이 크기 때문에 구름 분류가 어려운 것.
초기엔 기계학습 기반의 분류기로 구름을 분류하였다.
이후, 딥러닝 개발이 계속 이뤄지면서 이미지 분류 분야에서 컨볼루션 신경망의 성능이 계속해서 발전하였다.
특징 표현 능력이 뛰어나기 때문에 CNN이 사진으로부터 의미론적 특징을 잘 찾아낼 수 있었다.
(각각의 예시들은 skip)
기존 연구에서 참조할 수 있는 구름 이미지 데이터셋이 많다.
위성 구름 영상, 부분 지상구름 영상, 전천 지상구름 영상으로 분류
위성 구름 영상을 분류하기 위한 연구 방법들은 많이 나왔고 효과적임
하지만 위성 구름 영상은 넓은 영역을 커버하기는 하지만 국소 지역에 대한 디테일이 부족
따라서 태양광 생성을 위한 하늘의 패치 이미지를 분석하기에는 적합하지 않다.
부분하늘 구름영상은 시야가 좁기 때문에 대규모 PV 발전소에 적합하지 않다.
결국, 그림 1과 같은 전천 이미지를 사용하기로 함!
문제는 전천 이미지와 같은 유형의 구름 사진에 대한 연구가 적고, 이에 대한 데이터셋 크기가 매우 작다.
분류 정확도 또한 낮은 편이라 PV 전력 생성을 위한 응용 프로그램을 충족할 수 없다.
따라서,대용량의 지상기반 구름 이미지 데이터셋을 구축하고 딥러닝 기반 지상 기반 구름 이미지 분류 방법을 제안한다.
Main contribution
(1) National Renewable Energy Laboratory(NREL)에서 공개한 과거 구름 이미지 데이터를 수집하여 지상 기반 구름 이미지 데이터셋 NRELCD (NREL Cloud Dataset)을 구축하였다. 총 15450개의 이미지가 있고 7개의 카테고리로 분류.
(2) 결합된 신경망을 통해 새로운 지상기반 구름 이미지 분류 방법을 제안하였다. overlap pooling kernel을 사용하여 하위 네트워크에서 중복된 정보를 제거하는 효과를 향상시키고, 과적합 위험을 줄인다. 풀링 층 뒤엔 개선된 채널 어텐션 모듈 ECA-WS를 도입하여하위 네트워크의 채널의 특성 표현 능력을 향상시킨다. 하위네트워크를 개선하여 하위 네트워크 간 파라미터 최적화(기법?) 동기화. 결합 네트워크에서 두 하위 네트워크 출력에 가중치를 부여하여서 분류 정확도를 향상시켰다.
Related Work
<Deep Feature Extraction Network>
ResNet50과 VGG16은 깊은 특징들을 얻는 심층 컨볼루션 신경망이다.
ResNet50은 여러 Residual block들로 구성되어 있는데 각 residual block에 direct connection 채널을 추가했다.
잔여학습 알고리즘은 특징이 심층 네트워크를 타고 전파될때 정보의 손실을 줄일 수 있다. (아마 vanishing gradient 완화 얘기인듯)
VGG16은 크기가 큰 컨볼루션 커널을 여러개의 3*3 컨볼루션 커널을 쌓는 것으로 대체하여 네트워크가 수용영역은 유지한채로 더 복잡한 비선형 매핑 모드를 학습할 수 있도록 하였다.
Receptive Field (수용영역, 수용장)
각 단계의 입력 이미지에 대해 하나의 필터가 커버할 수 있는 이미지 영역의 일부
<ECA Attention Mechanism>
어텐션 구조는 객체의 중요도에 따라서 원래라면 균등하게 할당될 자원을 재분배할 수 있다.
다른 특징들간의 대비는 더 도드라지고 유용한 특징들은 더 중요해짐.
MAT, IHSM&EFRM, CBAM, SE, ECA등의 다양한 어텐션 메커니즘이 이미지 인식 영역에서 사용되었다.
MAT은 soft attention unit과 attention trainsition unit으로 구성되는데 이를 통해 attentive motion feature의 전환을 허용하여 각 컨볼루션 단계에서 apperance를 더 잘 학습하고, 시공간 객체 특징들을 풍부하게 만들어줌
이 모듈은 비디오 분석 작업에서 잘 쓰인다.
IHSM&EFRM은 인간-객체 상호작용 탐지 영역에서 사용되는데 각각 사람과 객체의 특징표현을 향상시킨다.
CBAM 모듈은 채널과 공간의 2중 어텐션을 포함하는데 다양한 차원에서 네트워크가 특징을 추출하도록 한다.
SE 모듈은 squeeze-excitation을 활용하여 각 채널간의 관계를 학습하고 각 채널에 다른 가중치를 부여한다.
차원 감소를 통해 모델 복잡도를 낮추었지만 이렇게 되면 채널과 가중치 간 direct correspondence가 떨어지게 된다.
ECA 모듈은 SE에 기반하여 차원 감소가 없는 local-cross channel interaction 전략을 제안하였다.
이 방법은 1D 컨볼루션 커널 사이즈를 적응적으로 선택할 수 있다.
ECA 모듈은 그림 2에서 확인할 수 있다. 이때 $\mathbf{X, X'}$는 각각 특징맵의 입력과 출력을 나타내며 $w,h,c$는 폭 , 높이, 채널 차원이다.
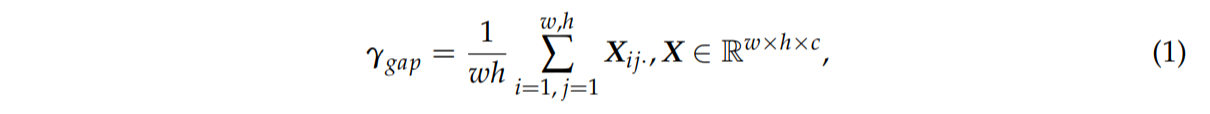
식 1을 통해 입력 특징맵 $\mathbf{X}$에 대해 전역 평균 풀링(GAP)을 적용하여 $1\times 1\times c$의 채널 코딩 벡터 $\gamma_{gap}$를 얻는다.
식 2에서 $\mathbf{V}_k^{gap}$는 띠 가중치 행렬이다. 채널 가중치 벡터 $\eta_{gap}$는 $\sigma$ (sigmoid) 함수를 통해 정규화되어 얻어진다.
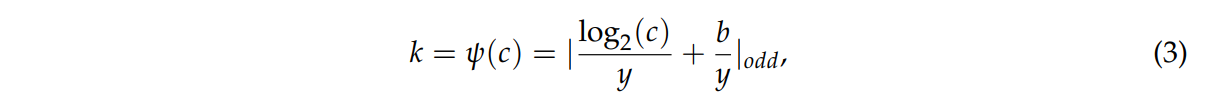
$k$ (kernel size)는 식3을 통해 계산되어 적응적으로 선택됨
이때 $\psi(\cdot)$는 $c$와 $k$사이의 매핑 함수를 나타낸다.
$|\cdot |_{odd}$는 가장 가까운 홀수를 의미한다.
$y, b$는 임의로 설정하는 매핑 파라미터이며 2와 1을 사용한다.
특징벡터는 1D 컨볼루션을 거쳐 얻는데 이때 원래 차원을 유지하게 된다.
<Decision Fusion>
같은 샘플에 대해서도 네트워크마다 분류 확률(네트워크 출력벡터)이 다르다.
이때 각 카테고리에 대해 출력 확률이 거의 같다면 네트워크가 샘플에 대해 좋은 판단을 내리기 어렵다고 볼 수 있다.
그림 3에서 처럼 여러 네트워크가 공동으로 결정을 내리면 샘플이 올바르게 분류될 확률이 증가한다.
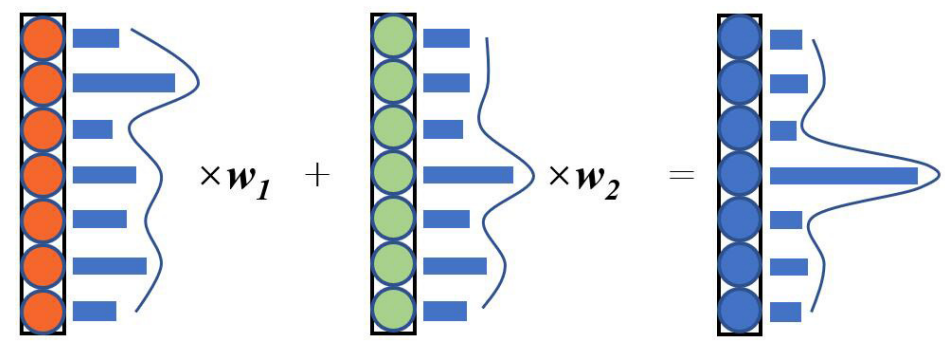
각 카테고리의 출력 확률이 거의 같다면 벡터에 작은 값을 곱하고, 반대의 경우에는 큰 값을 곱한다.
<Our proposed Methods>
모델은 다음의 4단계로 구성한다.
- deep feature combined network
- overlap pooling
- improved ECA module
- decision fusion
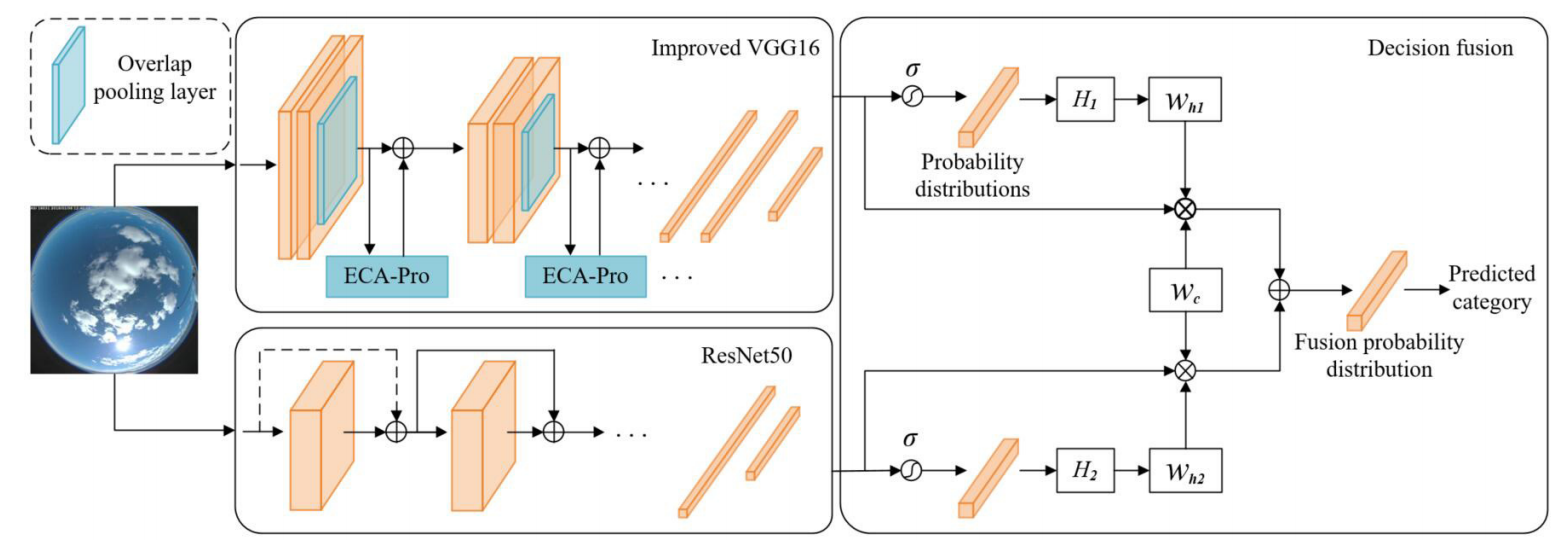
<Combined Network>
이때까지의 지상기반 구름 이미지 분류는 단일 채널 네트워크를 기반으로 한다.
하지만 특징 추출 성능에 제약이 있고 PV 전력을 예측하는 데에는 구름 이미지를 실시간으로 분류할 필요는 없다.
따라서 분류 성능을 높이기 위해 결합 네트워크를 사용하여 모델의 특징 추출 능력을 향상시킨다.
(실시간이랑 무슨 소리지? 단일 네트워크에 비해 속도가 떨어지나..?)
ResNet50과 VGG16 네트워크를 사용하여 이미지의 depth, width 특징을 추출한다.
ResNet50은 depth의 장점으로 구름 이미지에서 더 깊은 semantic 특징을 추출할 수 있다.
vgg의 경우 엄청 깊게 모델을 설계해도 어느순간부터는 성능이 늘지 않는데, resnet의 경우에는 깊게 쌓아도 성능이 향상되는 걸 의미하는걸까?
하지만 네트워크 크기가 첫번째 네트워크 너비와 높이의 4배로 확장되기 때문에 후속 컨볼루션에서는 이미지 특징이 일부 손실되기도 한다.
VGG16은 입력 차원 그대로 특징 추출을 수행할 수 있어서 높이/폭 차원에 대한 특징 추출 장점이 명확함
본 실험에서는 데이터셋의 용량이 적을때는 ResNet50의 결과가 훈련이 안정적이고 VGG는 과적합을 겪는 경향이 있어서 결과를 떨어트림. 이런 결과는 결정융합에서 바람직하지 않다.
결정 융합 알고리즘이 잘 수행되려면 두 하위 네트워크 간의 성능이 대체로 비슷해야 함
이런 점에서 풀링 레이어 구조와 ECA-Pro 모듈을 개선하여 VGG16의 정확도가 떨어지지 않도록 한다.
<Overlap pooling>
지상 기반 구름 이미지의 대부분은 구름 부분은 회색-흰색이며 배경 부분은 푸른색이다.
이 때문에 인접 픽셀들간의 유사성이 높아진다.
이 유사성으로 인해 다른 이미지에 비해 구름 이미지의 정보 중복성이 높아지고 VGG16이 과적합되기 쉬워짐
네트워크 파라미터 수와 오버피팅은 이미지 정보의 중복때문에 일어나고 특징맵 풀링으로 인해 줄일 수 있다.
하지만 2x2 풀링 커널은 중복성이 높은 이미지의 다운샘플링 퀄리티를 크게 향상시킬 수 없음
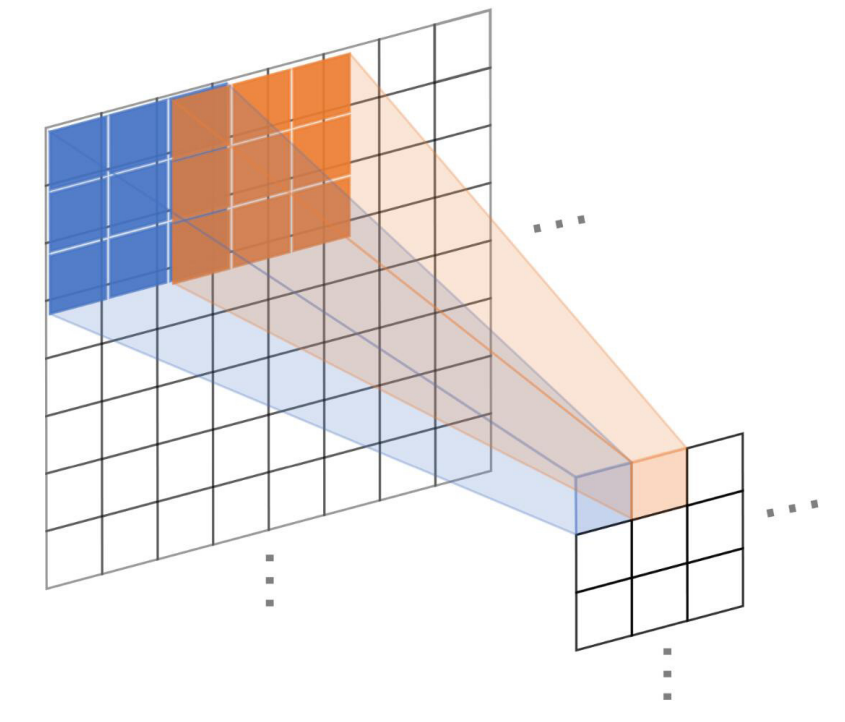
기존의 풀링 커널 대신 크기 3*3의 풀링 커널을 사용한다.
중복된 특징들은 제거되고 인접한 수용영역의 일반적인 특징이 추출된다.
pooling step은 2로 설정하여 풀링커널이 인접한 수용영역을 교차(overlap)할 수 있도록 한다.
크기는 3인데 step을 2로 하면 1만큼이 겹쳐지게 됨
이로 인해 특징의 상관성과 네트워크의 과적합 억제가 이뤄진다.
<Improved ECA>
그림 1의 구름 이미지 샘플을 보면, 전천 이미지를 획득하기 때문에 이미지 내의 원형 부분만 유효하고 주변에 검은 픽셀로 이루어진 코너 4개는 불필요하다.
GAP가 노이즈를 억제하는 기능이 있는 건 맞지만, 이 이미지에 효과는 없을 것
이를 해결하기 위해는 전역 평균 풀링(GAP)이 아닌 전역 맥스 풀링(GMP)을 사용하여 특징 계산할 때 불필요한 부분의 개입을 막는다.
이로 인해 채널 특징 추출 능력을 어느정도 향상하였다.
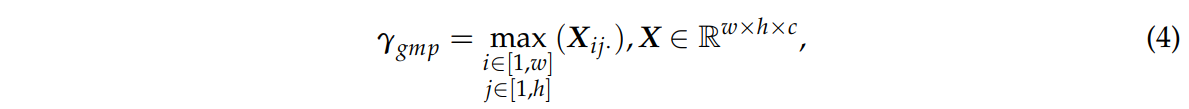
식 4를 통해 GMP를 계산한다.
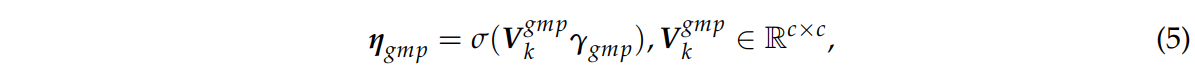
전역 평균 풀링에서와 같이 $\gamma_{gap}$에 띠 가중치 행렬 $\mathbf{V}^{gmp}_k$를 곱한다.
그렇게해서 채널 가중치 벡터 $\psi_{gmp}$를 출력으로 얻음
ECA 어텐션 모듈을 풀링 레이어에 맞댄다. GAP와 GMP는 $\mathbf{X}$의 전역 특징을 공동으로 추출
GAP와 GMP는 병렬로 사용되어 두 특징맵의 공간정보를 모은다.
만약 GAP가 GMP 이전에 수행되면 GMP연산 이후 특징 맵에서 최대값보다 작은 모든 값들이 버려지게 되는데, 이때 버려지는 것들은 GAP에서 처리한 유용한 정보다.
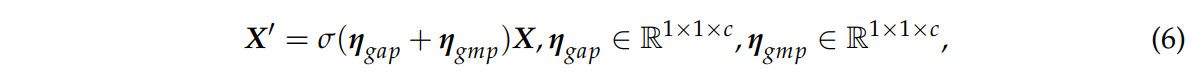
$\mathbf{X}'$는 전체 어텐션 모듈의 출력을 나타낸다.
ECA 모듈에서 GAP와 GMP를 조합하는 방법이 두 가지 있다.
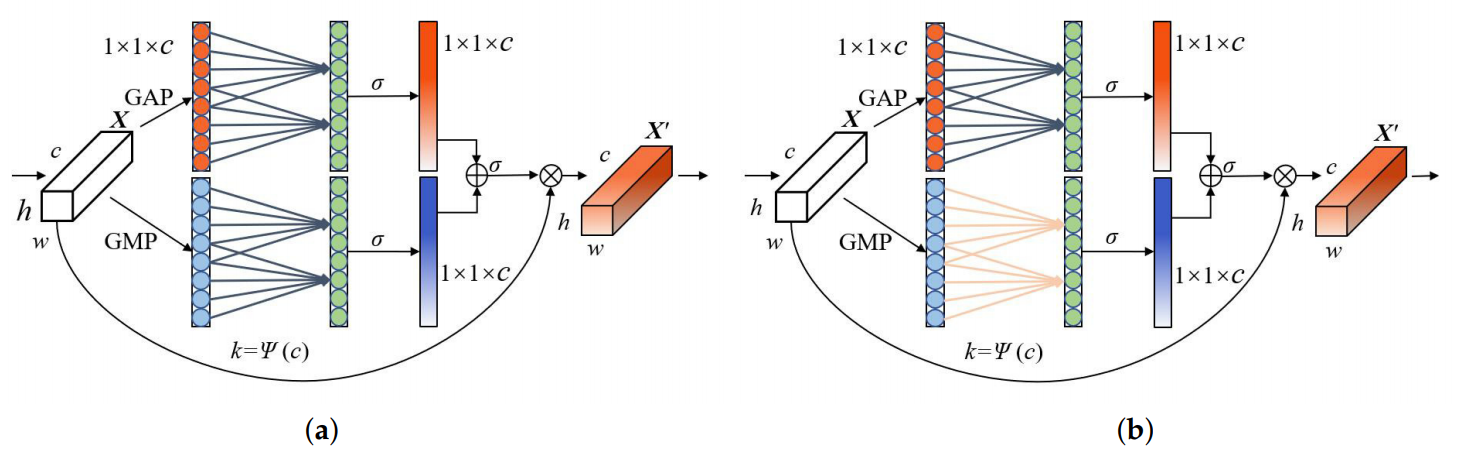
그림 6의 a,b를 각각 weight sharing method (ECA-WS), weight independent method (ECA-WI)로 명명하였다.
ECA-WS에서는 GMP가 GAP와 같은 띠 가중치 행렬을 갖는다. 즉, $\mathcal{v}_k^{gap}=\mathcal{v}_k^{gmp}$
ECA 모듈의 파라미터는 거의 유지한 채로 모듈의 특징 추출 기능을 향상시킨다.
ECA-WI에서는 GMP가 GAP와 다른 띠 가중치 행렬을 공유한다. 즉, $\mathcal{v}_k^{gap}\neq\mathcal{v}_k^{gmp}$
이 방법은 네트워크의 파라미터를 증가시키면서 두 전역 풀링간의 상관성을 줄인다.
매번 풀링 이후에 vgg16 하위 네트워크의 채널 특성의 특성화능력(characterization ability)를 향상시키기 위해 ECA-WS 어텐션 구조를 사용한다.
<Decision Fusion>
분류 성능을 개선함에 있어서 여러 네트워크를 융합하는 것의 효과가 크기 때문에 가중 알고리즘(weighted algorithm)을 도입하여 두 하위 네트워크의 결과를 융합한다.
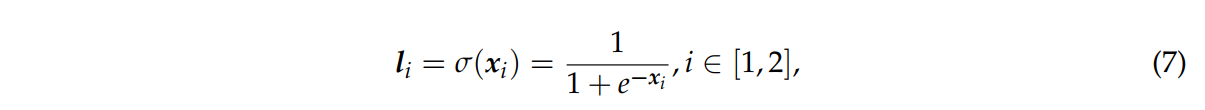
먼저 $\sigma$함수로 각 네트워크의 출력값을 정규화한다.
이때, $x_i$는 $i$번째 하위 네트워크의 출력 벡터를 의미한다.
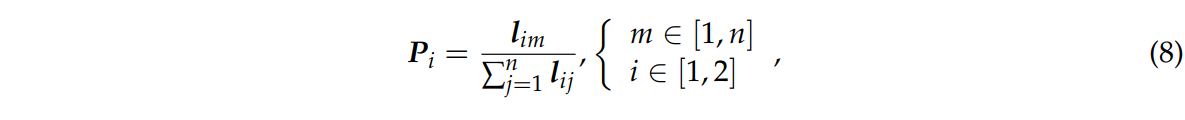
식 8은 정규화된 확률 분포를 나타낸다.
$\mathbf{P}_i$ : 네트워크의 확률 벡터 출력
$\mathbf{l}_{im}$ : $m$번째 카테고리의 값
$n$ : 구름 이미지 카테고리 개수출력 확률 행렬은
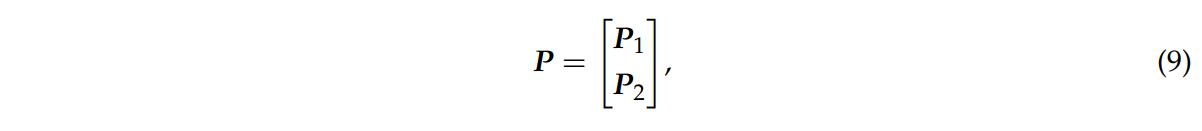
변환된 결합 네트워크의 출력 확률 행렬은 식9처럼 표기한다.
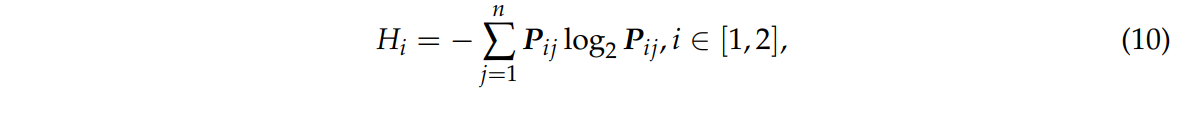
이후에, 식 10은 각 네트워크 출력의 확률 분포인 정보 엔트로피 (information entropy)$H_i$이다.
정보 엔트로피가 커질 수록 네트워크 예측 결과의 불확실성이 커지고 잘못 분류할 확률이 높아진다.
따라서 가중치를 작게 할당해야 한다.
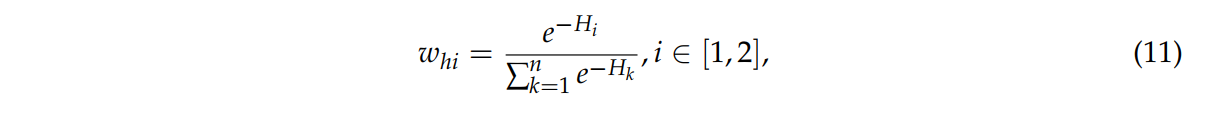
식11은 하위 네트워크의 가중치 $w_{hi}$ 이다.
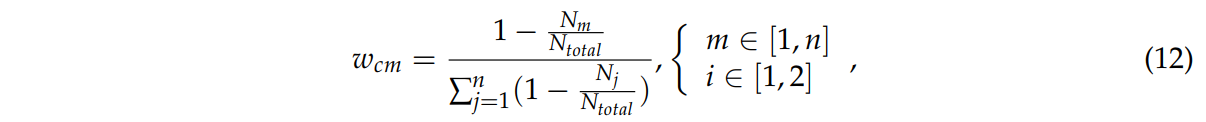
식 12는 카테고리의 샘플 수에 따른 각 카테고리의 가중치 $w_{cm}$이다.
$N_m$ : $m$번째 카테고리의 샘플 수
$N_{total}$ : 전체 샘플 수
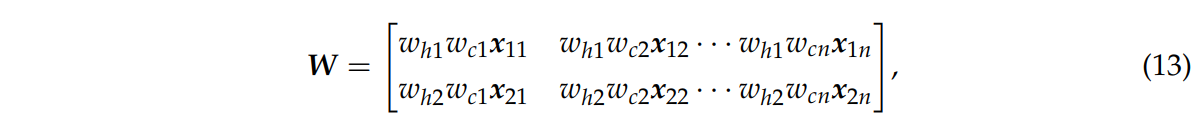
하위 네트워크 가중치 $w_{hi}$와 카테고리 가중치 $w_{cm}$을 원래의 입력 $\mathbf{x}$에 곱한다.
식 13은 결합 네트워크의 가중된 행렬 $\mathbf{W}$
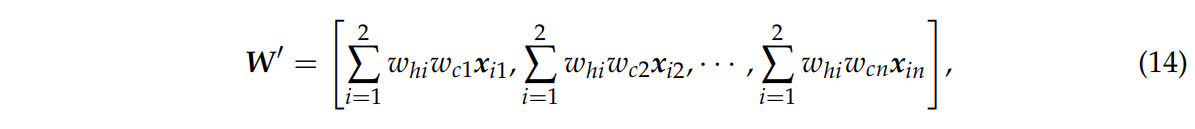
모든 행끼리 더해준다.
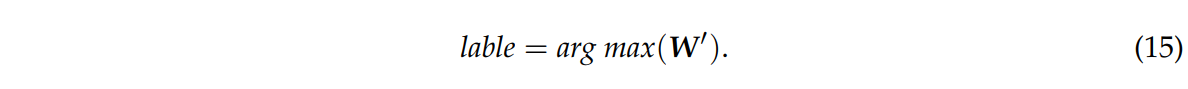
열에서 최댓값을 갖는 인덱스를 선택하면 이것이 최종 분류 결과이다.